An der Hohenzollernbrücke, auf der die Züge kurz vor Einfahrt in den Kölner Hauptbahnhof den Rhein überqueren, hängen eine Vielzahl sogenannter Liebesschlösser: Vorhängeschlösser, die von einem Liebespaar dort angeschlossen und deren Schlüssel dann in den Fluss geworfen werden. Jedes Mal, wenn ich nach Köln fahre, wundere ich mich über die schier unglaubliche Menge an Schlössern. Bei meiner letzten Köln-Reise, aus Anlass der Ausstellung zu Sigmar Polke, habe ich mich konkret gefragt: Wie viele Schlösser mögen dies wohl sein?

Diese Frage bin ich dann „physikalisch“ angegangen, d.h. ich habe eine „Messung“ gemacht: ich habe also versucht, die Messgröße „Anzahl der Schlösser“ mit vertretbarem Aufwand zu bestimmen, wobei ich mir der dabei vorhandenen Messfehler bewusst bin. Der naheliegende Ansatz, nämlich „einfach alle Schlösser abzählen“ scheidet aus Zeitgründen für mich aus: Dafür sind es viel zu viele! Also mache ich stattdessen einige „Stichprobenzählungen“ an mehreren Stellen auf der Brücke und reche dann auf die gesamte Brücke hoch. Für diese Stichproben bieten sich die einzelnen, gut einen Meter breiten Segmente (im Folgenden „Felder“ genannt) des Zaunes zwischen dem Fußweg und den Bahngleisen an, an dem die meisten Schlösser hängen.

Aber bereits in jedem einzelner dieser Felder hängen zu viele Schlösser, als dass ich sie einzeln zählen möchte, also zähle ich die Schlösser in einem schmalen (vertikalen) Abschnitt eines Feldes und schätze davon ausgehend die Schlösser in diesem Feld insgesamt. Die Ergebnisse dieser „Messung“ an neun Feldern sind im folgenden Diagramm zu finden:

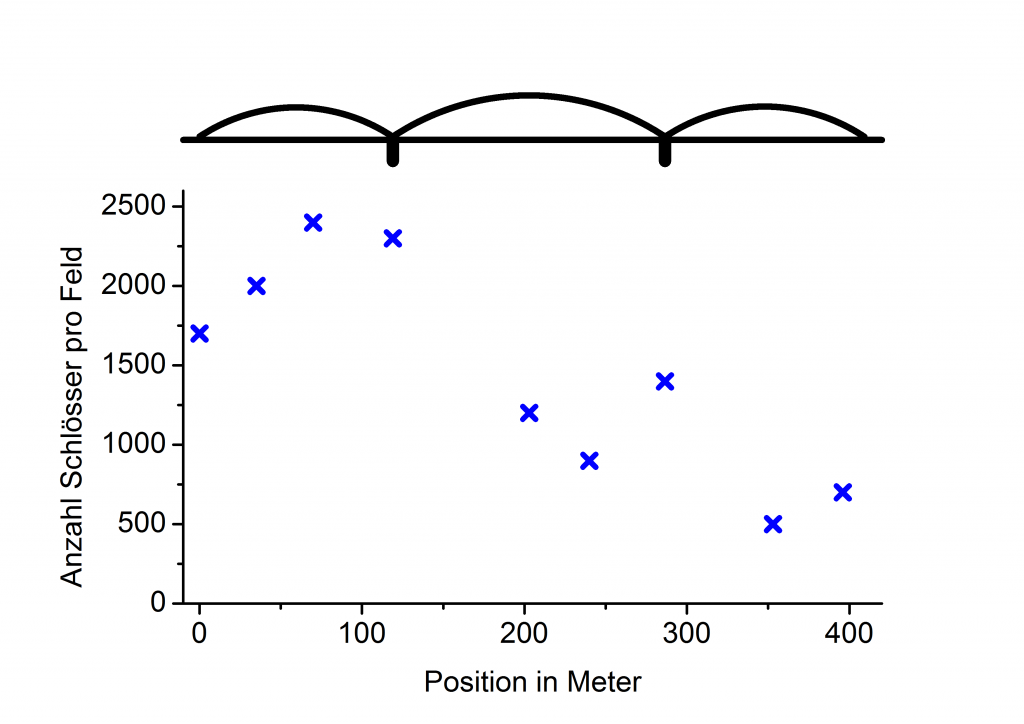
Es ist klar zu erkennen, dass die Dichte der Schlösser sehr unterschiedlich verteilt ist: Zur linken, westlichen Seite hin hängen deutlich mehr Schlösser als zur rechten, östlichen Seite hin. Das ist insofern schlüssig, als vermutlich viel mehr Paare von der Kölner als von der Deutzer Seite zum Schlossanbringen auf die Brücke gehen und eben nicht bis zur Mitte der Brücke gehen, sondern schon vorher einen passenden Ort finden.

Auch ist an „besonderen“ Stellen, etwa genau auf den Brückenpfeilern (zwischen mittlerem und seitlichen Brückenbogen) oder genau in den Mitten der drei Bögen die Dichte höher es etwas abseits davon: Diese Stellen sind sicherlich praktisch für solche Liebespaare, die sich die Stelle, an der „ihr“ Schloss hängt, merken bzw. wiederfinden wollen.

Diese ungleiche Schlösserdichte macht es natürlich schwerer, von der vorhandenen Datenlage auf die Gesamtzahl der Schlösser zu folgern. Wenn ich trotzdem eine mittlere Anzahl der Schlösser pro Feld abschätze und mit der Anzahl der Felder multipliziere, erhalte ich 450.000, also etwa eine halbe Million Schlösser!

Wie groß ist der „Messfehler“ bei dieser Schätzung? Er ist relativ groß, denn einerseits ist die Anzahl der „gezählten“ Felder zu klein für eine gute Statistik entlang der gesamten Brücke. Dann ist jeder „Messwert“ (also Schlösser pro Feld) bereits eine Schätzung (wobei der wahre Wert gerade bei den dichtbehängten Feldern eher höher als „mein“ Wert sein wird als niedriger), außerdem ist die „Anzahl der Felder“ ebenfalls nicht klar definiert (es gibt an den Schrägen der Brückenbogen diverse kleinere Felder) und schließlich gibt es noch Schlösser, die nicht in den Feldern hängen (sondern irgendwo dazwischen oder darüber, außerhalb der eigentlichen Brücke oder auch auf der – viel weniger benutzten – Nordseite der Brücke, die ich hier nicht berücksichtigt habe). Dementsprechend wird die Anzahl größer sein als der obige Wert und der Messfehler groß.

Meine Schätzung für die Anzahl der Liebesschlösser an der Hohenzollernbrücke am 6. Juni 2015 lautet somit:
500.000 ± 200.000
Also die bereits genannte halbe Million Schlösser. Was für eine hohe Anzahl!

Was für Schlussfolgerungen kann man aus dieser Zahl ziehen? Einige Gedanken dazu hier.

Falls sich der Leser über eine so ungenaue Zahlenangabe durch einen Physiker wundert: Ein solches Vorgehen ist ein wichtiger Teil unserer täglichen Forschungsarbeit! Wenn wir auf eine neue Fragestellung stoßen, schätzen wir zunächst grob ab, in welcher Größenordnung sich das Ergebnis befindet. Hier etwa: Sind es eher 1000, 10.0000, 100.000, 1.000.000 oder 10.000.000 Schlösser? Auf Basis der ersten Abschätzung können wir dann weitersehen: Reicht uns dieser Wert oder wollen wir es genauer wissen? Und wenn wir es genauer wissen wollen, haben wir bereits einen Eindruck davon, wie groß der Aufwand für eine genauere Messung sein wird und ob dieser für das Beantworten der jeweiligen Frage gerechtfertigt ist.
Ein berühmtes Beispiel für ein solches schnelles Abschätzen von Zahlenwerte sind die „Fermi-Abschätzungen“, deren Name auf Enrico Fermi zurückgeht.